1.10 F-value

The F-value is the ratio of the variance between the groups to the variance within the groups. The between-groups and within-groups degrees of freedom affect F’s exact shape. We plot three F distributions as follows:

fVals <- seq(from=0.01,to=5,by=0.01)  # Make a sequential list of F values
# Plot the density function for this scenario
plot(fVals, df(fVals,df1=2,df2=57))
# Add points to the same plot, different df1
points(fVals, df(fVals,df1=3,df2=57))
# Add points to the same plot, different df1
points(fVals, df(fVals,df1=4,df2=57))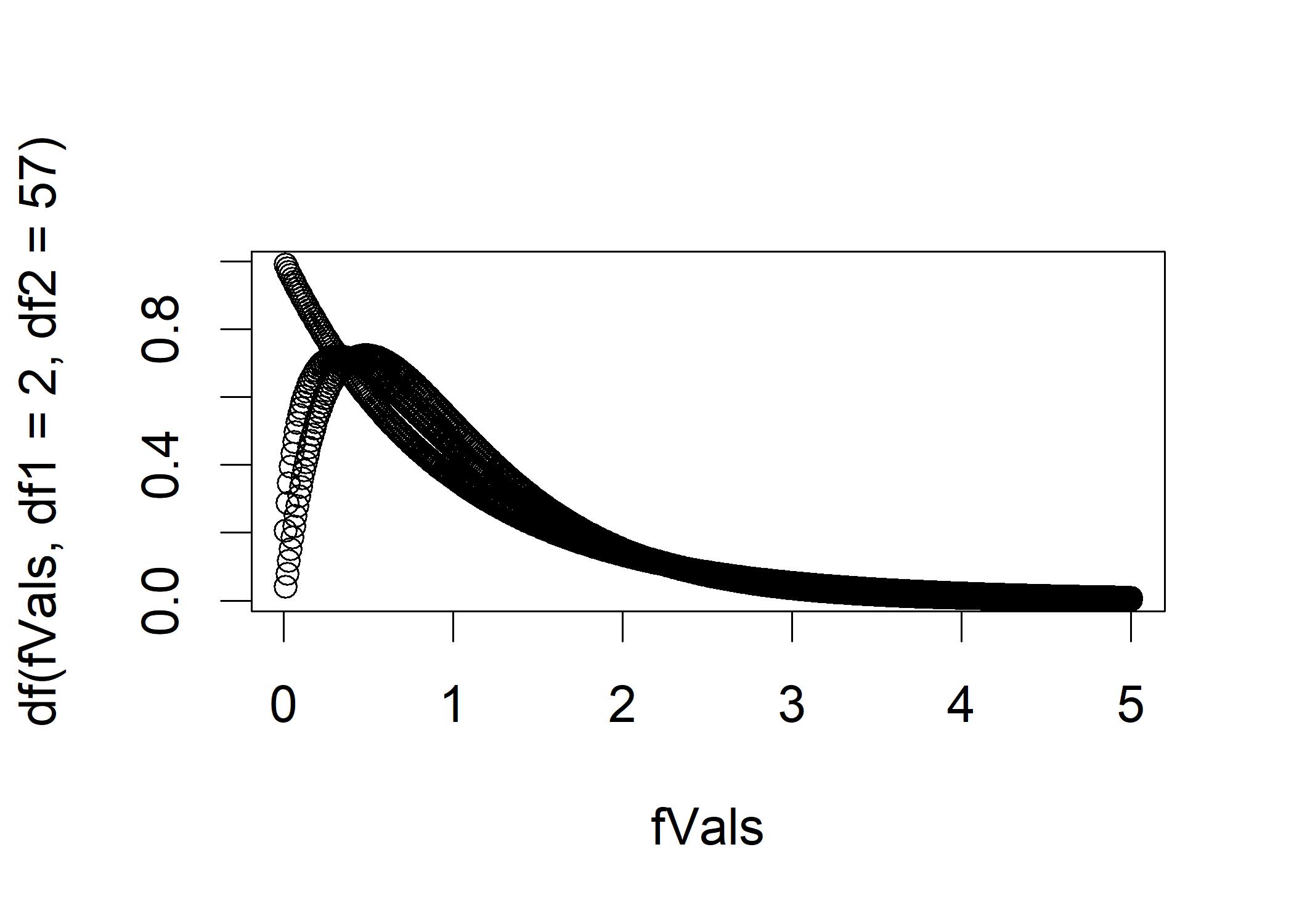

Each point on the density curve shows the percentage of F-values that would be seen at a specific level of F, if the null hypothesis were to hold.

BASIS FOR COMPARISON	T TEST	F TEST
Meaning	T-test is a univariate hypothesis test, that is applied when standard deviation is not known and the sample size is small.	F-test is statistical test, that determines the equality of the variances of the two normal populations.
Test statistic	T-statistic follows Student t-distribution, under null hypothesis.	F-statistic follows Snedecor f-distribution, under null hypothesis.
Application	Comparing the means of two populations.	Comparing two population variances.